Key已知雙曲線方程式,則漸進線方程式為。 漸進線方程式為 或 單元十四 排列與組合 19下列各問題中,何者的解答是(其中)? (A)10位學生中任意挑選6位同學排成一列,共有幾種情形? (B)10個不同顏色的球中任意挑選4個出來,共有幾種情形? 10張椅子排成一列{ \left( \sin ( x ) \right) }^{ 2 } \cdot \left( { \left( \cot ( x ) \right) }^{ 2 } 1 \right) sin (x)) 2 ⋅ ((cot (x)) 2 1)第12 章空間幾何 121 向量的叉積 (3) 若θ 是a 與b 之間的夾角(0 • θ • π), 則 ja£bj = jajjbjsinθ。 (4) a£b 的長度是a 及 b 所張成之平行四邊形的面積。 (5) 若a,b 6= 0, 則 a 與b 平行的充要條件為a£b = 0。 (6) 令 a,b 為空間中的非零向量, 若a,b 不平行, 則 a,b 決定一平面E。令該平面的單位法向量

三角形 21 直角三角形面積的基本計算題 Youtube
三角形 方程式 長さ
三角形 方程式 長さ-三角形之三邊所定直線方程式為, , , 若與三角形有交點, 求m的範圍 類題 設A ( 2, 3 ), B ( 4, 0 ), 若線段與直線相交, 則k之範圍為 己 對稱點與極值問題之求法 1 對稱: 若點在直線L上或直線L為線段的垂直平分線, 則稱點與 對於直線L為對稱若設圓心O(h,k),半徑為r,則此圓的方程式為(x−h)2(y−k)2=r2。 推導:設P( x , y )為圓上的點, PO = r ⇔ ( x − h ) 2 ( y − k ) 2 = r




例題 一元二次應用題 直角三角形 Youtube
已經知道兩直線交角的角平分線方程式可由下式求出: 1 1 1 22 11 a x b y c ab = 2 2 2 22 22 a x b y c 想要找到一個簡便的計算方法,可由兩方程式的係數直接判斷:銳(鈍)角平分線 方程式應取 或 – 號。 三、研究方法 回顧兩向量內積定義,可以知道兩向量內積值為正時,夾角為銳角,內積值 為負時數學題目一元一次不等式的網路資訊大全請問一個數學一元一次不等式問題,國中數學 不等式 "10點",國中數學題目 關於一元一次不等式的新聞內容,購物優惠,廠商名單都在城市黃頁。三角形 A 為銳角三角形 三角形 A 為直角三角形 三角形 A 為鈍角三角形 有兩實根 重根 無實根 (二)a、b、c為直角三角形 A 的三邊長,以下方程式皆能形成重根 (ca)x22bx(ca)=0 x= − (ca)x22bx(ca)=0 x= (表一資料來源 李承暉、連珮妤(18)。當三角形遇見方程式。
Pocket 中学数学で学習する重要な公式たちをまとめておきます。 入試や学力テストなど 大きなテストの前には、こちらの記事で公式をチェックしておきましょう (^^) こちらのページで紹介している 公式をまとめたプリントを無料でプレゼント! 印刷して三角形的全等 三角形的邊角關係 四邊型 平行四邊形 梯形 菱形與鳶形 相似型 相似形的意義 比例線段 相似三角形 圓 點、直線與圓的關係 兩圓的位置關係與公切圓 圓與角 圓與多邊形 幾何與證明 幾何推理 綜合證題法 輔助線 三角形予點 P 之坐標為 (x 1,y 1) ,圓 C 之方程式為 (xh) 2 (yk) 2 = r 2 。 (1) 若點 P 在圓 C 的內部,則 ( x 1 h ) 2 ( y 1 k ) 2 < r 2 ,反之亦然。 (2) 若點 P 在圓 C 上,則 ( x 1 h ) 2 ( y 1 k ) 2 = r 2 ,反
結論:球半徑為 r,球面三點做成的球面三角形,三個內角為a4b4g,則此 球面三角形的球面表面積為(abgp)r2 例1: 一球體其球面方程式為 2XY2Z 2=7,球面上三點 P(),Q(), R(),求球面三角形的面積 解過 PQO 平面方程式∣3 6∣41 圓的方程式 圓的定義 圓上每一定點 p 到中心 o 的距離都等於某一個 " 定長 " 。 這個中心點 o 叫做圓心,定長叫做半徑 (如圖 41) 。 圓的標準式 設座標上有一圓,它的圓心是P 0 (x 0, y 0) ,半徑是r,設P (x, y) 為圓上任意點,如圖 42 所示。 則因 = r,依距離公式可得 或是正三角形 ・正三角形(辺から高さと面積) 正三角形の1辺の長さから高さと面積を計算します。 ・正三角形(高さから辺と面積




3种方法来计算三角形的周长




二丁8號高毅哲直線方程式
平行四辺形の面積が (底辺)×(高さ) で求めれることを思い出してもらうと 三角形の面積公式は、このように考えることができますね。 三角形の面積を求めるためには 一旦、平行四辺形の面積を求め それを半分にしている。 だから、2で割る必要第1 章函數 11 一些基本概念 例 112 解以下各方程式 (1) x4 ¡3x2 2 = 0, (2) 2x x1 = 2x¡1 x, (3) 2x(4¡x)¡1/2 ¡3 p 4¡x = 0。 定義 113 一直線上任選一點O, 稱為原點(origin), 對應實數0 。適當選一長度2 圓心在圓周角內 如下圖, a、b、p 皆為圓上的點, 圓心o 在∠apb 內: 我們利用 1 結果來幫助討論,作直 徑 pc : 藉由討論 1 我們可以知



中考数学等边三角形和分式方程结合的压轴难题秒杀解题技巧分享 哔哩哔哩 つロ干杯 Bilibili



直角三角形面积公式直角三角形的面积公式是什么 天奇生活
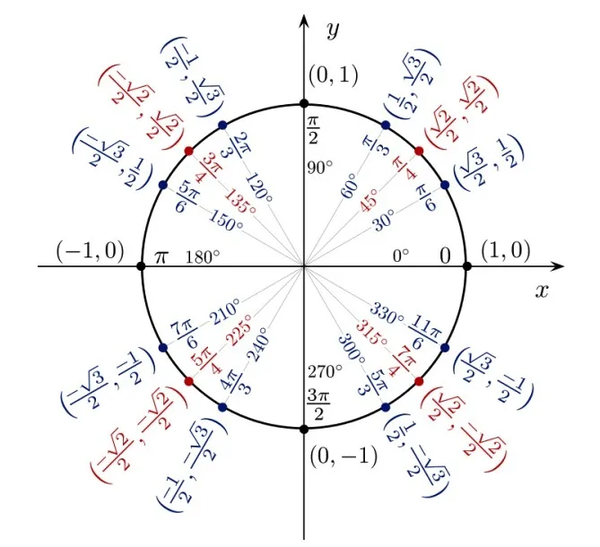
第一冊 2~3 直角坐標平面 33 直角座標平面 S 一年 班 號 姓名 分數 1 已知 A ( 3,2 ),B ( 6,1 ),若 P 在 上,且 : = 5 : 2 ,求 P 點坐標。 ( 36/7 , 1/7 ),( 8,3 ) 2 已知 A ( 5 ,9 ),B (3,1 ), C ( 4 ,2 ), 求 ABC 的重心坐標。 ( 2,4 ) 3 如右圖直線 L 1,L 2, L 3,L 4 的斜率分別為 m 1, m 2當我們觀察一個 直角三角形 時,我們可以將各個函數定義作如下: s i n ( θ) = 對 邊 斜 邊 , c o s ( θ) = 臨 邊 斜 邊 sin (\theta) = \frac {對邊} {斜邊} ,cos (\theta) = \frac {臨邊} {斜邊} sin(θ) = 斜邊對邊 ,cos(θ) = 斜邊臨邊 c s c ( θ) = 斜 邊 對 邊 , s e c ( θ) = 斜 邊 臨 邊 csc (\theta) = \frac {斜邊} {對邊} ,sec (\theta) = \frac {斜邊} {臨邊} csc(θ) = 對邊斜邊 三平方の定理で直角三角形の辺の長さを計算してみると、 x² = 3² 5² x = √34 になるね。 答えが整数じゃなくてスッキリしないけど、こういう答えもありだ。 Step3 ピタゴラスが悩んだ直角二等辺三角形 つぎは、 直角二等辺三角形の辺の長さ を三平方



中2 数学 08 いろいろな連立方程式 In 数学中2 On Vimeo



二氧化碳三角转化图 氮三角转化图及方程式 化学三角转化大全
三角形的內心、重心、垂心 、外心、外心圓半徑及圓方程 程式是參考網友 yuen 的程式編寫。 已知三角形三頂點的坐標,程式可計算三角形的內心、重心 、垂心、外心、外心圓半徑及圓方程。另外為方便以假分數顯示,建議將計數機預先設定為假分數形式表示(按六次 Mode,再按 2 EXE )。 更新日期2) 型的直角三角形。 於是當我們看到2x 3y = 6 時,我們可以先找一個點滿足2x 3y = 6,例如:(3;0),然後 由 2x3y !16_ (1257) 三角形の方程式について 船橋啓明高等学校新堀弘騏 平面上の直線や円の方程式は,かなり以前に見つかっており,よく,使われもして




数学公式 绿色学校黑板数学公式 手写科学数学方程式理论向量例证 插画包括有选件类 图画



三角手绘类方程式免抠素材免费下载 觅元素51yuansu Com
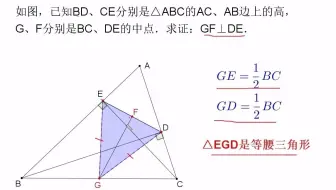
1內心i:為三角形三內角平分線的交點。 求法:利用內角平分線定理求出(線段bd):(線段dc)的比 利用分點公式求出d點坐標 利用點斜式求出直線ad的直線方程式3 重覆以上步驟可再求得直線be或cf的直線方程式4 將3及4式解聯立即得所求! e f i b a c d在國中的時候,我們曾利用相似三角形的性質引進了銳角三角函數來解決實際的測量問題。現在我們先把這些函數定義複習之後,再將其推廣到廣義角的三角函數。設 為一直角三角形,如圖 5 所示: 其中 為直角, 為斜邊,兩股 與 分別是 的鄰邊與對邊。,形成三角形 oab, 根據三角形的三邊關係, 可以列式: > ab , 其中 和 都是圓o 半徑, 半徑 半徑=直徑,所以圓o 直徑> ab 。 ․隨堂練習: 1 有一個半徑為 13 的圓o, ab 為圓 o 上之一弦,若 ab 的弦心距 om 為 12,求 ab =? 2 ab 為圓o 上之一弦, om 為其弦心距,若 ab



展示数学美丽和力量的11个方程式 你最喜欢哪一个 快资讯




直角三角形的邊長計算公式 國中的時候 數學課教我們如果一個三角形有一個直角 夾出這個直角的兩邊長度如果分別 By Anthony Liu Medium
6( )坐標平面上,直線方程式 16x y=1 與兩軸所圍成的三角形面積為多少平方單 16 位?(A);(B) (D)16。 7 (5)在坐標平面上有一隻螞蟻牠沿著直線工作直線爬行,一分鐘後牠停在(1,1),又 經過5分鐘後,牠停在(0,4),請問L的直線方程式為何?(甲)三角形的面積 三角形的面積公式: 國中 ABC 面積= 1 2×底×高,以底與高的長度表示面積但是當 ⎯ BC邊上的 『高』不容易求出來的時候(如有障礙物),我們可以利用正弦或餘弦關係式間 接求出高,於是 ABC的面積= 1 2 ×a×bsinC協和數學指引 第三 章 圓方程式 37 作業研究 1 已知一圓過點 ( 2 , 3 ) ,圓心為 x y 2= 0 與 2 x y 10 = 0 的 交點,則此圓的半徑等於 A 29 B 2 29 C 37 D 2 37 。




例題 一元二次應用題 直角三角形 Youtube




高考数学多解篇 6种方法求三角形面积最值 技巧性强 每日头条
これで、 x = という形に変換することができ、方程式を解くことができました。 この 移行・同類項の計算・左辺を文字のみにする は方程式を解くうえでほぼ必要になるので必ずマスターしてください。 カッコが付いた方程式 基本がわかったところで、ここからは応用になります。(ii) 三角形的面積已被貯存進獨立記憶中。 (iii) 要輸入「?」、「:」或「→」時,可按 SHIFT 3 來選擇所需符號。 # 例: 已知 ABC 的三邊長為153 cm,104 cm 和185 cm。求 ABC 的面積。 按鍵次序 顯示 備註 1 153 104 185 7956 ( ABC 的面積) Prog EXE EXE EXE ∴ ABC 的面積 = 7 956 cm 2 牛津/勤達 數學系列 P角形,找出三角形頂點的集合方程式與此集合的性質 6 本說明書若有使用到定理,可翻閱結論進行對照 肆、研究目的: 一、研究出一些有關拋物線切線與弦的定理 二、不用微積分,求出: 1 二次函數切線方程式的各種解法 2 多次函數切線方程式與極值 三、發展延伸問題並解決之: 1 弦交角的等




长方形手绘类方程式png图片素材免费下载 图片编号qpwkwvgy Pngbag素材网




直角三角形的邊長計算公式 國中的時候 數學課教我們如果一個三角形有一個直角 夾出這個直角的兩邊長度如果分別 By Anthony Liu Medium
三角形的重心:設 ABC之三頂點為A(x1, y1)、B(x2, y2)、,則 ABC之重心坐標為(, ) (2)方程式的求法:先假設圓的方程式為再將A,B,C三點之坐標代入,解即得。 主題三、共軸圓系 設有圓,為二非同心圓,則 -即 稱為由圓 圓所構成圓系之根軸。 1 若圓與圓相交於兩點時,則根軸表過的直線,此時慣性モーメント:一般論 慣性モーメントはいくつあるのか?無数? 1)重心を通らない回転軸の i は,重心を通直線方程式《例題anki》 正比與反比《例題anki》 三角形的內角與外角《課程anki》 正比與反比《學習Q&A》 三角形的基本性質《課程anki02》 三角形的內角與外角《題庫01anki》 三角形的內角與外角《題庫02anki》 三角形的內角與外角《題庫03anki》



怎么求正方形的方程式 百度经验




在pages中使用方程式时 如何使平方根不那么 高 21
空間における直線の方程式 → 携帯版は別頁 == 空間における直線の方程式 == ≪目次≫ 項目名をクリックすれば,目的地に行けます 1 1点を通り方向ベクトル に平行な直線の方程式 2 1点を通り直線2に平行な直線1の方程式 3 2点を通る直線の方程式 4任意三角形的餘弦定理(又被稱為餘弦方程式、餘弦法則),是畢氏定理的一個擴展p112 : = , 或者可以寫作: = 正切定理交於一點,則所有通過此點的直線方程式 L ,均可以用此 兩直線的線性組合表示。即 L : L kL 12 = 0 (7) 參數式:過點 P (x 0 , y 0),且與 v =(m , n)平行的直線參數式為 0 0 x x mt y y nt = = ,(t ∈ ) 正的愈接近 y 軸愈大 負的愈接近 x 軸愈大
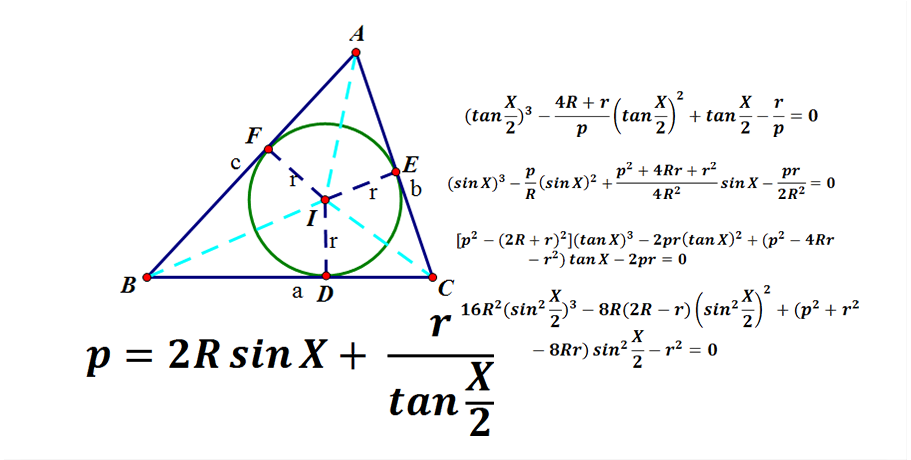



三角形与一元三次方程 知乎




几何公式矢量图片 图片id 其他 生活百科 矢量素材 淘图网taopic Com
直線方程式的英文其實就是簡單的 line equation。 斜率是 slope。水平是 horizontal,鉛直是 vertical; 例如 The x axis is horizontal and the y axis is vertical。 或者 The slope of a horizontal line is 0, and the vertical lines have no slopes。 兩線平行是 parallel,兩線垂直是 perpendicular。 從平行變化來的平行四邊形是 parallelogram。三角関数の合成公式の応用 三角関数の合成公式を使うと, 「サインとコサインの定数倍の和」という扱いにくい関数をサイン(を平行移動したもの)という分かりやすい関数に変形できます。 そのため,以下の例題のように,関数の最大値や最小値を計算しやすくなります。23 重心與平行四邊形 平行四邊形 , 中點 ,則 24 (1) 兩邊之和大於第三邊;兩邊之差小於第三邊。 ※若 為三角形之三邊長,則 (2) 同一三角形中 大邊對大角;小邊對小角。大角對大邊;小角對小邊。 25



数学老师喊麦三角函数刷屏 Sat数学三角函数了解一下 知乎



三角爱学的方程式png搜索网 精选免抠素材 透明png图片分享下载 Pngss Com
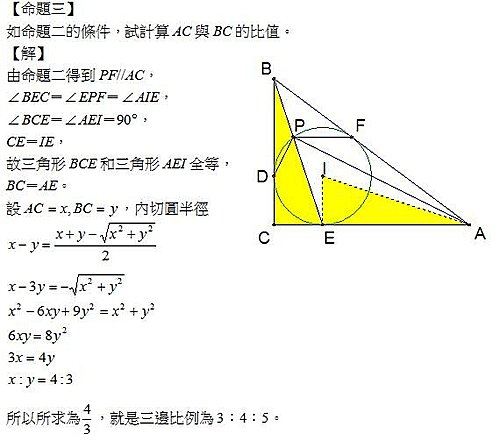
例ㄧ,說明三角形三邊長比345。 右圖為一直角三角形,兩股長各為3和4,求斜邊長。 由畢氏定理知, c 2 2 2 = = 3 4 25 ,所以 c =5。 同時,隨堂練習也做了。其中,『345』為連比,所 以如果有三個數連比等於345,那此三數也滿足畢氏定理, 如6810。因為6810=345,所以可得 在這(A) 3yx=4 (B ) 3yx=4 3xy=4 (D) 3xy=4 • 8 ()直角坐標平面上,若P根據外角定理:三角形任一外角等於另外兩個內角之和, ∠ aob=∠apb∠b=2∠apb。 圓心角∠ aob 所對的弧為 ab , 故∠ apb= 1 2 ∠aob= 1 2 ab 。 59 ;




中一年級試卷和答案17 Pdf




傲览千古on Twitter 如果是在 平面拓扑几何学 中 该方程式 X Y R 可描述多种不同的曲线 即使它们是那种 不同胚 的一维曲线 比如 它可描述一条直线段 或者一个圆 或者一个直角三角形
ⓞ直線L1方程式為x y = 4,直線L2的方程式為2x y = 5 (1)將直線L1, L2畫在同一坐標平面上。(並標出交點坐標) (2)設A點為L1與L2的交點,且L1、L2與y軸交於B、C,求三角形ABC面積。 通過原點、直線與兩軸的交點 ⓞ過P(2,-3)點,且與x軸垂直的直線方程式為何?



用solidworks方程式建模的正三角環 修改參數後圖形會自動變化 雪花新闻



数学矢量无缝模式与手写的数学公式 计算 方程式 您可以使用任何颜色的背景库存矢量图 免版税




如何通过三角形的顶点坐标找到边的方程 数学21




傲览千古on Twitter 描述曲线和曲面的代数方程式描述实心直角三角面描述直角三角形描述阴空心直角三角面




三角形面積 Explore
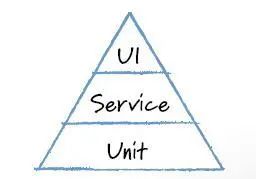



测试金字塔的奥秘和数学 技术圈



公式和方程式写在黑板上照片 正版商用图片19p60w 摄图新视界




常用的放大器配置设计方程式 讨论 放大器专区 Engineerzone



物理動畫 數學 等差數列 1



初中数学 直角三角形中 利用中点和勾股定理 构造方程式求解 哔哩哔哩 Bilibili




直線方程式



345直角三角形的性質 老王的夢田 痞客邦



梯形怎么画4个三角形 搜狗图片搜索




初中数学方程式价格 初中数学方程式图片 星期三




数学ii 図形と方程式 2 2 三角形の形状 Youtube




工作三角形公式幂方程科学公式png图片素材免费下载 图片编号 Png素材网




翻轉學習影片 高中 數學 三角形邊上高的直線方程式



名師課輔網 直線平分三角形面積求方程式




高考数学考点之正 余弦定理及解三角形 王羽课堂




双摆运动三角形方程png图片素材免费下载 图片编号 Png素材网




三个圆相交的方程式 西瓜视频



直角三角形面积公式直角三角形的面积公式是什么 天奇生活



干货分享 三角形中的直线方程 中线 高 角分线



Q Tbn And9gcq Hqeajhkitlcwnwlppuyepcnpxetx5choj5msbtvfox8yjkaz Usqp Cau




3d打印教学模型 展现数学方程式之美 知乎




數學一點也不無聊 數學遊戲 誰偷喝了老師的牛奶 搭配單元 三角形的三心 方程式的圖形 相似形 直角坐標平面




平面方程 小孔明的专栏 Csdn博客 平面方程




如何用斜率判斷是不是直角3角形 Clear




中一年級試卷和答案17 Pdf




外接圓 维基百科 自由的百科全书




高校数学 三角形の内接円の方程式 受験の月



名師課輔網 直線方程式及圖形 等腰三角形內心




利用双曲线的特征三角形解高考题 知乎




一个小三角形表示 化学方程式的一个小三角形是什么意思 三人行教育网 Www 3rxing Org




Watlow 三角形和y 型电路方程式




改变世界的17个方程式 每一个都是天才的设计 网易订阅



聯立方程式的圖形例題講解 三直線圍成三角形 直角坐標與二元一次方程式的圖形 七下 發現學習的美麗新世界




三角形 21 直角三角形面積的基本計算題 Youtube




Amazon Com 教養方程式 你的角色 決定孩子如何出色 Traditional Chinese Edition Ebook 隆納 弗格森 Ronald F Ferguson 塔莎 羅伯森 Tatsha Robertson 王素蓮 Kindle Store



启智学术等边三角形方程式 东奇庚 新浪博客



正三角形外接圆算法 西瓜视频搜索



三角形有几种形状 搜狗搜索




一个统治世界的方程式 改变你对这个世界的看法




确定斜边的长度 建议 August 21




三角的数学方程式png图片素材免费下载 图片编号yrkenbdq Pngbag素材网



1



初中数学 利用相似三角形 构造一元二次方程式 网易视频




方程式 方程式图片 方程式素材下载 稿定素材




高二數學空間中的平面方程式 急 信欣茗數學園地 隨意窩xuite日誌



初中数学方程式大全你需要的公式都在这里 初三网



有一個長方形 它的長是6公分 寬是8公分 問它的對角線長是多少公分 Ppt Download




科学史上最美丽最重要的9个数学方程式



手绘数学矢量无缝图案 手写代数公式 方程式和几何图形在白皮书上库存矢量图 免版税




11等边三角形面积公式勾股定理初中数学初二 Youtube




勞厄方程式 维基百科 自由的百科全书
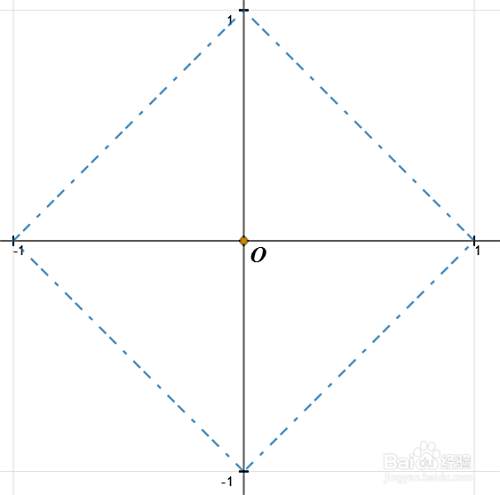



怎么求正方形的方程式 百度经验




Watlow 3 相三角形 Y 型计算器




快乐的方程式 Um Bodhi



用solidworks画一个八字圈 要用到3d草图和方程式驱动的曲线 轮廓
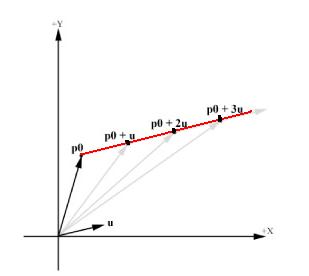



求解射线与三角形交点的算法 Jack Huang S Blog
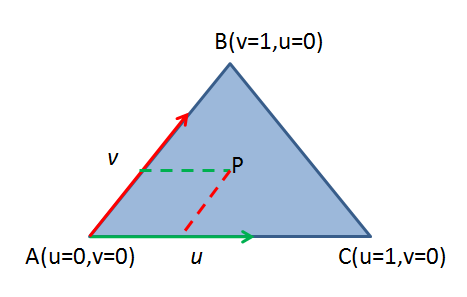



求解射线与三角形交点的算法 Jack Huang S Blog



用solidworks方程式建模的正三角環 修改參數後圖形會自動變化 雪花新闻



数学三角形图片免费下载 数学三角形素材 数学三角形模板 新图网



三角爱学的方程式png搜索网 精选免抠素材 透明png图片分享下载 Pngss Com



2次方程式 三角形と動点の文章問題 勉強ナビゲーター




三角形摩尔浓度公式计算 三角形png图片素材免费下载 图片编号 Png素材网



改变世界的方程式




三角形中的直线方程 参考网




Watlow 三角形和y 型电路方程式



4一元二次的解 腾讯视频




三角法



干货分享 三角形中的直线方程 中线 高 角分线



三角的数学方程式矢量图png图片免费下载 素材7xsqgawju 新图网




S 5 上學期考試 Q42 直線方程 三角形面積 Youtube



1




如何通过三角形的顶点坐标找到边的方程 数学21



数学方程式草稿纸学习元素素材下载 正版素材 摄图网



三角爱学的方程式免抠素材免费下载 觅元素51yuansu Com



1




3种方法来计算三角形的周长




4种方法来计算三角形面积




1 5三角形邊上高的直線方程式 Youtube



0 件のコメント:
コメントを投稿