題名を見て、うっとなった方、数学恐怖症の方、ご覧にならない方がよいかもしれません。(笑) そうでない方は、是非ご覧ください! 中3の頃、三平方の定理を習いたての頃、 「3以上のすべての奇数において、3辺が整数となる直角三角形の1辺になることができる」ということを見つけ
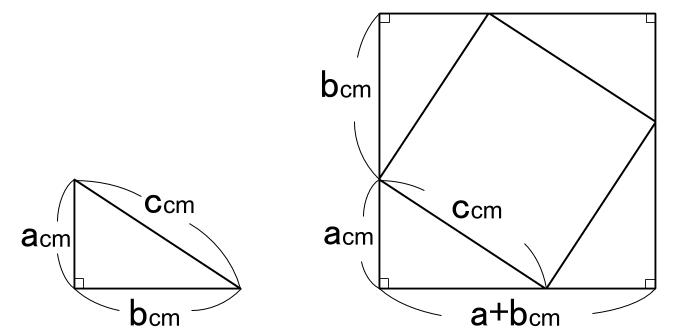
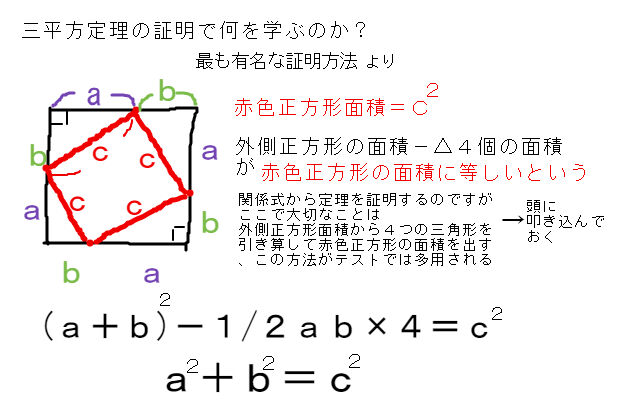
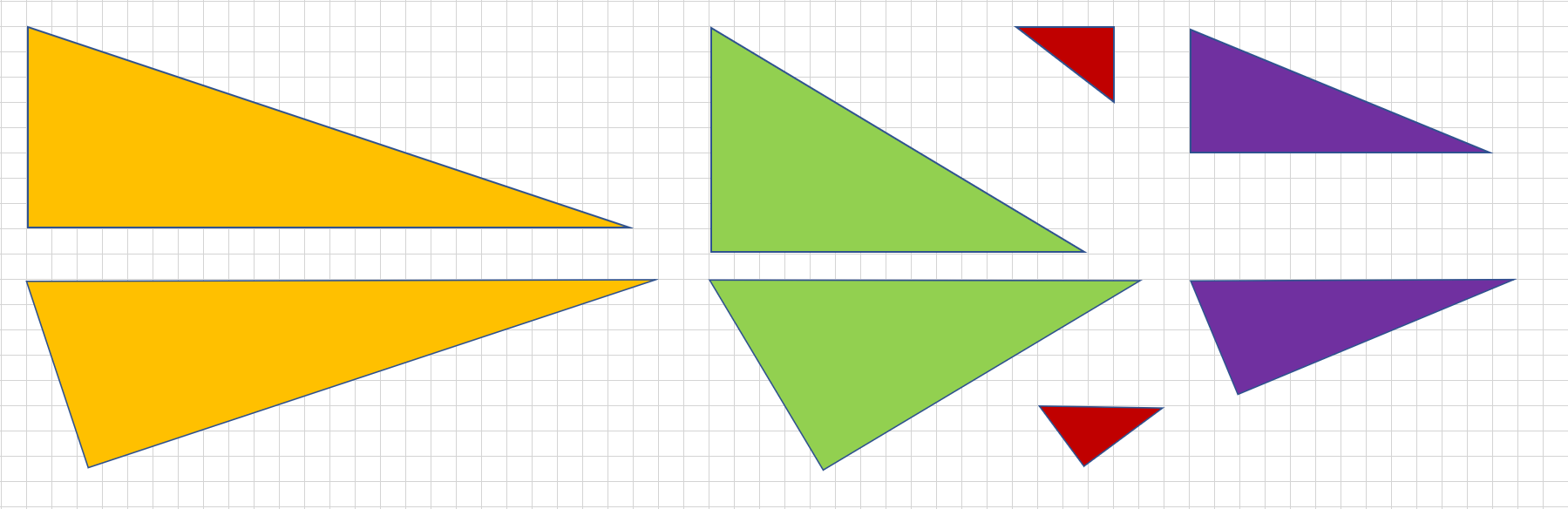
中学数学 三平方の定理 解説-三平方の定理(ピタゴラスの定理)は中学3年間のまとめ分野になります。 教科書に出てくる定理は1つだけで覚えるのも簡単です。 長さを求める定理なので、面積、体積を求める問題に使うことが多くなります。 三平方の定理が直接問題三平方の定理 定理 直角三角形の斜辺を 辺 として、残る直角をはさむ二辺を 辺 および 辺 とした場合に となる。 (証明) 図のように直角三角形 ABC を4つ適切な位置に配置すると、 一辺の長さを a+b とする正方形 EFGHをつくる事ができる。 このとき、正方形 DBAE の面積は、正方形 EFGH の面積から、直角三角形 ABC の面積4つぶん を差し引いた面積に等しい。 したがって よって (証明 おわ
中学数学 三平方の定理 解説のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  | |
 |  | |
「中学数学 三平方の定理 解説」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「中学数学 三平方の定理 解説」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | |
「中学数学 三平方の定理 解説」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  |  |
「中学数学 三平方の定理 解説」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
 |  |  |
「中学数学 三平方の定理 解説」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 | 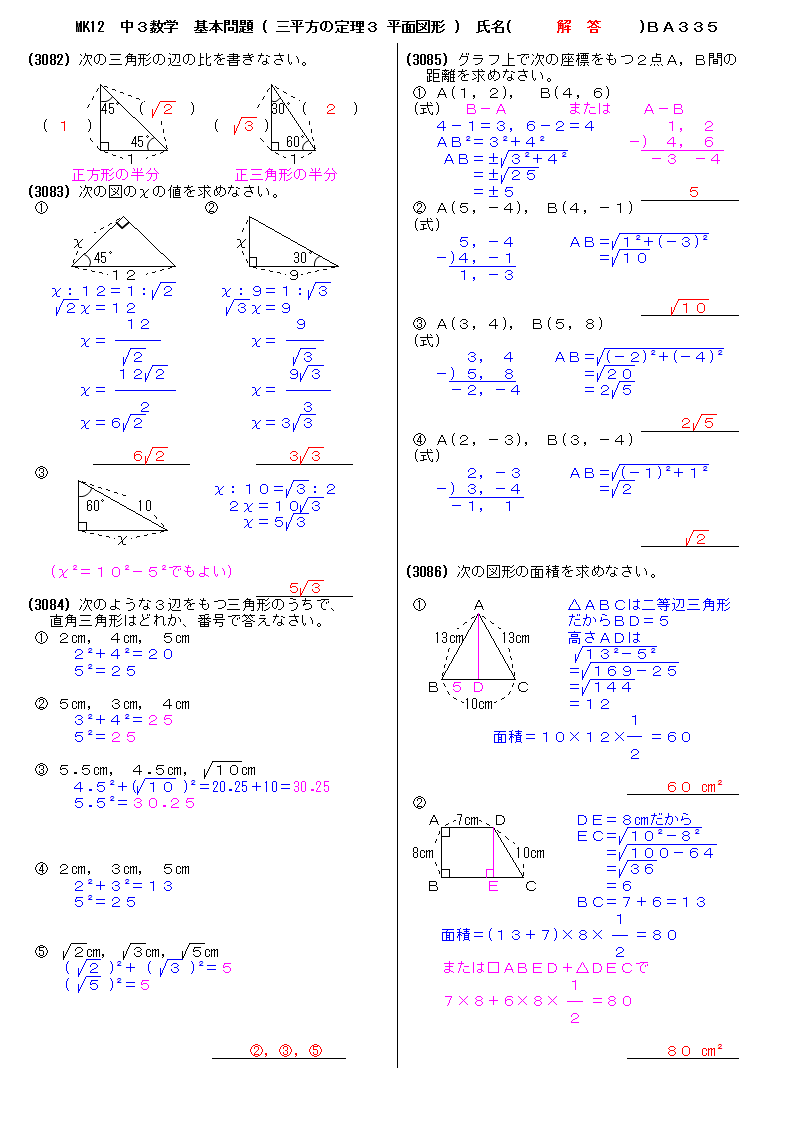 | |
「中学数学 三平方の定理 解説」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  |  |
「中学数学 三平方の定理 解説」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  |  |
「中学数学 三平方の定理 解説」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |
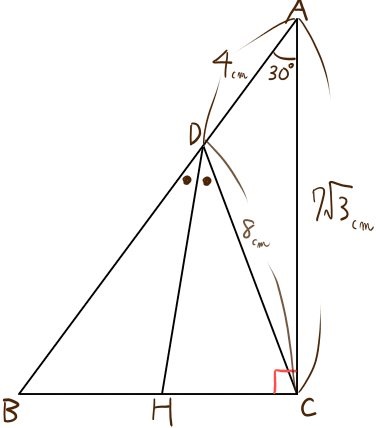
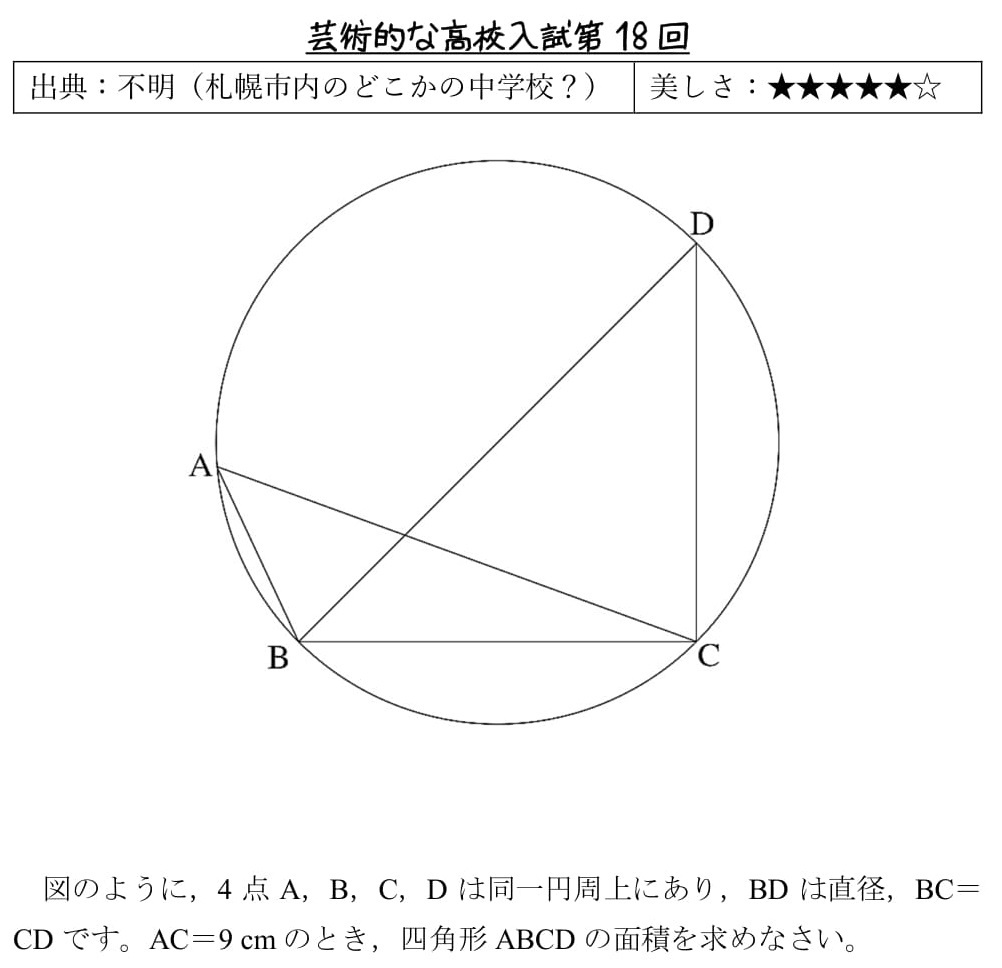
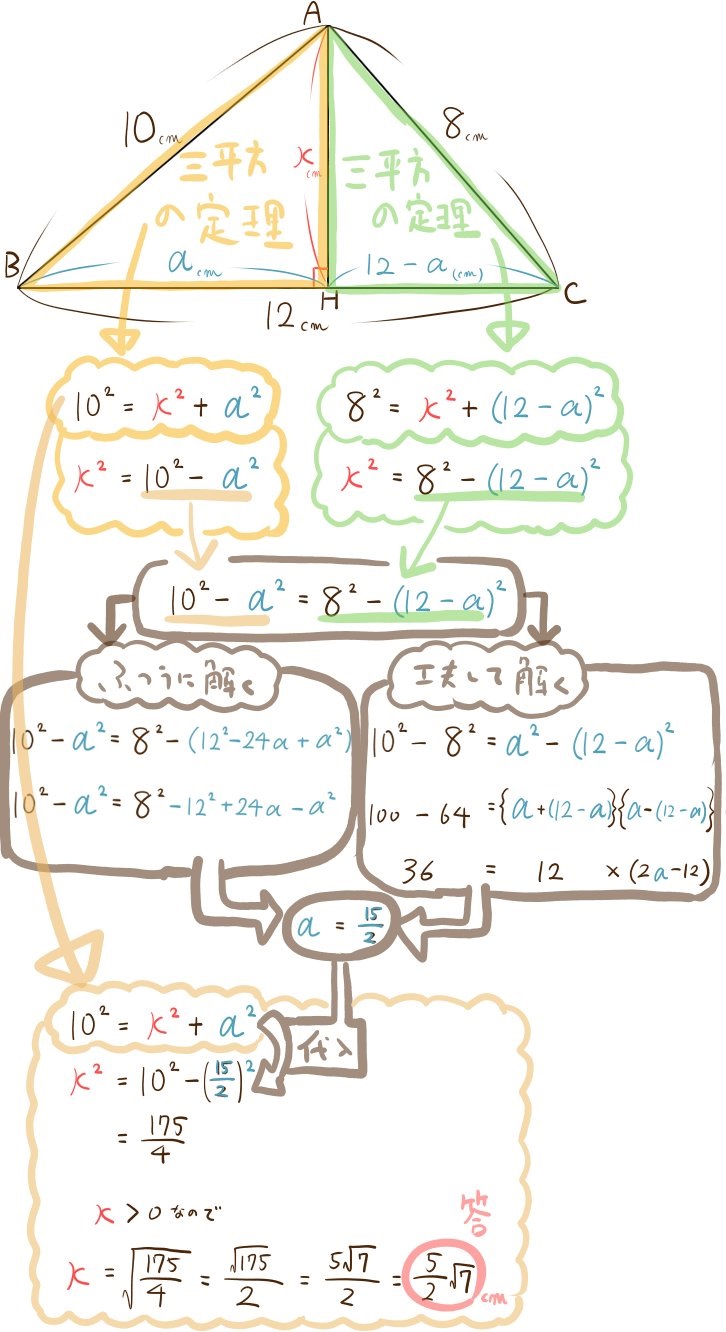
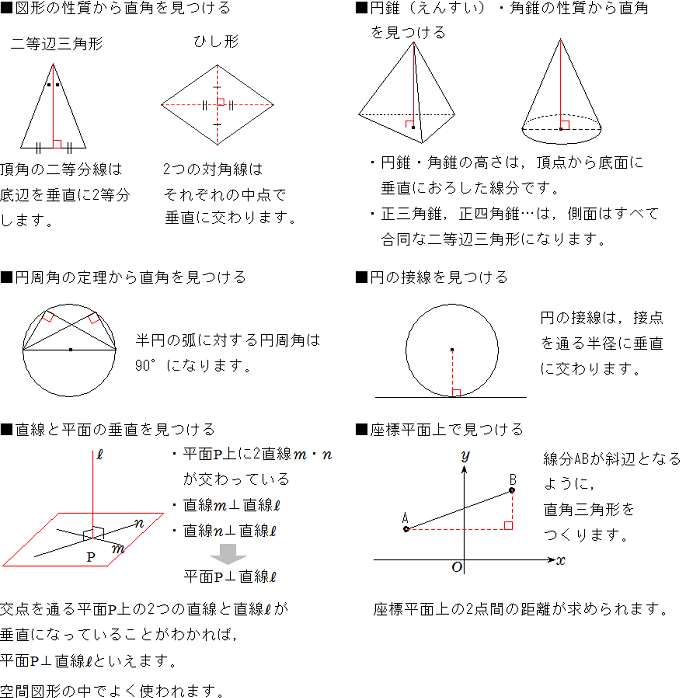
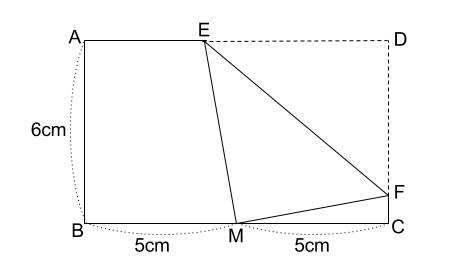
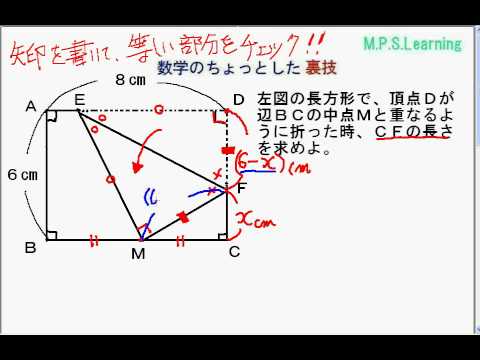
三平方の定理とは、 「不思議な直角三角形」の不思議さを説明したもの です。 直角三角形は、上の図のような形をしていて、内側の 3 つの角のうち、 1 つが 90 度になっています。 90度(直角)を挟む辺の長さを b 、 c として、斜辺を a とすると、次の関係が成り立ちます。 a 2 =b 2 c 2 a 2 は「 a の二乗」といい、「 a × a = a2 」と表記します。 a 2 =b 2 c 2 の関係が成り立つのこの問題は直線DEを書くだけで、基本的な三平方の定理の問題になります。 DE=8cm,EC=4cm ですので、 x = 8 2 4 2 x = 64 16 x = 80 x = 4 5 解答 x = 4 5 cm 三平方の定理 解説まとめ 今回は基本的な問題で、三平方の定理の問題の解き方のポイントを伝えました。 きっと学校ワークの問題も解けるハズ! 似たような問題でも、繰り返すうちに理解が深まったり、計算が早くなったりします
Incoming Term: 三平方の定理 中学数学, 中学数学 三平方の定理 応用問題, 中学数学 三平方の定理 問題, 中学数学 三平方の定理 空間図形, 中学数学 三平方の定理 比, 中学数学 三平方の定理 証明, 中学数学 三平方の定理 解説, 中学数学 三平方の定理 公式,




0 件のコメント:
コメントを投稿